O fundamental em Sala de Aula: a medição da constante de Planck Teach article
Traduzido por Pedro Augusto. Traga a descoberta para a sala de aula e mostre aos alunos como medir a constante de Planck utilizando equipamento simples.

Akimbomidget/Wikimedia
Quando pensamos na medição de constantes físicas fundamentais, tais como a velocidade da luz ou a força da gravidade, é provável que nos ocorram experiências famosas feitas em larga escala – mas o equipamento da sala de aula pode também ser utilizado para estimar estes valores não variáveis.
A constante de Planck pode parecer um conceito bastante vago em oposição, por exemplo, à velocidade da luz, mas desempenha um papel absolutamente central na compreensão do comportamento da matéria a nível subatómico. É uma pedra basilar da teoria da Mecânica Quântica que descreve o estranho comportamento das partículas a esse nível. Aqui a energia, bem como a matéria, é composta de partículas. A luz e outra radiação eletromagnéticaw1, por exemplo, é composta de partículas chamadas fotões.
Imagem em Domínio
Público/Wikimedia
Assim designada em honra do físico alemão Max Karl Planck (1858-1947), a constante de Planck diz-nos como a energia dos fotões individuais se relaciona com o comprimento de onda da respetiva radiação, como a seguinte equação-chave mostra:
Ep = hc/λ
onde Ep é a energia de um único fotão (em joules), h é a constante de Planck, c é a velocidade da luz no vácuo e λ é o comprimento de onda da radiação.
Talvez de forma surpreendente, apesar do valor da constante de Planck ser extremamente pequeno, nós desenvolvemos um método para a determinação do seu valor numa experiência em sala de aula. A atividade não necessita de equipamento especial – apenas uns poucos díodos emissores de luz (LEDs, do inglês: light-emitting diodes) e um aparato elétrico padrão. Esta atividade é adequada a uma gama larga de estudantes, dos 16 anos ao nível pós-graduado.
Como funcionam os LEDs
Os LEDs são produzidos pela junção de dois materiais semicondutores ‘dopados’, um dos quais tem um excesso de eletrões (tipo n), enquanto o outro tem um défice – também designados de buracos (tipo p). Quando uma corrente elétrica é injetada através desta, assim chamada, junção ‘p-n’ a recombinação de eletrões e buracos liberta energia na forma de fotões.
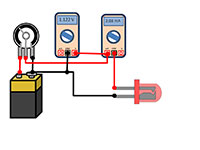
medição da resposta
voltagem-corrente de cada
LED. Da esquerda para a
direita: pilha, potenciómetro
ou reóstato, voltímetro,
amperímetro, LED.
A imagem é cortesia dos
autores.
A cor da luz emitida por um LED é determinada pela energia dos fotões, que pode ser ajustada pela alteração da composição química dos materiais semicondutores. Os LEDs são usualmente feitos de ligas de gálio, arsénio e alumínio e alterando a proporção destes constituintes podem-se produzir LEDs que emitem luz com cores específicas – tais como vermelho e verde na região visível do espetro eletromagnético – ou mais além, para dentro das regiões ultravioleta e infravermelha.
Para qualquer tipo de luz, é o seu comprimento de onda que determina a sua cor. O olho humano é sensível a luz com comprimentos de onda de cerca de 390 a 700 nanómetros (0.00039-0.0007 mm). Vemos os comprimentos de onda mais curtos como violeta e os mais longos como vermelhos e, entre estes, cada um corresponde a uma cor particular do espetro. Por exemplo, os LEDs que emitem no verde produzem, tipicamente, luz com um comprimento de onda de cerca de 567 nanómetros.
Utilizamos LEDs nesta experiência pois cada cor de LED tem uma voltagem-fronteira à qual os eletrões começam a ser produzidos. Em conjunto com os valores tabelados para os comprimentos de onda de emissão, medindo esta voltagem encontramos o caminho para a descoberta do valor da constante de Planck.
Materiais
- Quatro LEDs que emitam luz colorida – um de cada: vermelho, laranja, verde e azul. Escolha LEDs com um invólucro transparente e incolor em seu torno de forma a garantir que a cor da luz vem do dispositivo e não do invólucro colorido.
- Pilha de 9V.
- Dois multímetros (um para ser utilizado como voltímetro e o outro como amperímetro)
- Um potenciómetro ou reóstato de 1kW.
Procedimento
- Monte o circuito como mostrado no diagrama acima. Ligue o amperímetro em série com o LED para medir a corrente que o atravessa e o voltímetro em paralelo, de forma a medir a sua voltagem. A voltagem aplicada pode ser alterada utilizando o potenciómetro ou reóstato.
- Altere a voltagem em passos de 0.05 V de 0 V a 3 V e meça a consequente corrente elétrica. Note que quando a corrente que atravessa o LED é pequena este pode nem acender, mas o amperímetro ainda consegue medi-la. De forma a proteger o LED, deve-se manter a corrente abaixo dos 5 mA.
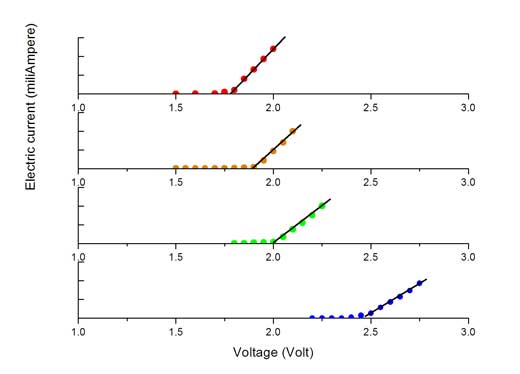
- Para cada LED construa um gráfico corrente-voltagem, semelhante aos gráficos apresentados à esquerda. Em cada gráfico, encontre a reta que melhor ajusta os pontos que se vão afastando do eixo dos xx. Se os pontos estão próximos da reta, isto mostra que existe uma relação linear entre a voltagem aplicada e a corrente nesta região do gráfico.
- Finalmente, determine a voltagem de ativação (Va) a partir dos dados recolhidos. Este é o ponto onde a corrente começa a aumentar de forma linear com a voltagem. Pode ser lida do gráfico por extrapolação para trás da reta que representa a resposta na região linear até que se interseta o eixo dos xx. Os alunos podem fazer isto visualmente com a utilização de uma régua ou matematicamente com a aplicação de regressão linear aos pontos experimentais na região de linearidadew2.
A imagem é cortesia dos autores
De forma a obter os valores mais precisos de Va para cada cor de LED, pode calcular um valor médio utilizando os resultados obtidos por vários alunos.
Os valores típicos para voltagens de ativação obtidos através desta experiência apresentam-se à direita, junto com os comprimentos de onda da luz emitida pelos LEDs coloridos. Pode fornecer estes valores de comprimentos de onda aos alunos para a fase seguinte da atividade em sala de aula. Alternativamente, os comprimentos de onda podem ser medidos utilizando um espetrómetro feito em casa, tal como o descrito no recurso web abaixo apresentadow3.
| Cor do LED | Comprimento de onda típico, l (cm) | Voltagem de ativação, Va (V) |
|---|---|---|
| Vermelho | 623 | 1.78 |
| Laranja | 586 | 1.90 |
| Verde | 567 | 2.00 |
| Azul | 567 | 2.45 |
A imagem é cortesia de entirelysubjective/Flickr
Análise e resultados
Como vimos antes, a energia dos fotões emitidos, Ep (medida em joules), está relacionada com a constante de Planck (h), a velocidade da luz no vácuo (c) e o comprimento de onda desta (l):
Ep = hc/λ (1)
Nesta experiência, temos uma gama de valores para l dos comprimentos de onda conhecidos das cores dos LEDs e sabemos o valor de c (2.9979 x 108 ms-1). Mas como utilizar os nossos valores de Va obtidos experimentalmente para o cálculo da constante de Planck? Para o descobrir, consideremos o que está a acontecer dentro dos LEDs.
Quando os LEDs operam a valores de voltagem baixos, a entrada de energia não é suficiente para produzir fotões e a corrente elétrica é muito pequena. A uma certa voltagem, o LED começa a emitir fotões: esta é a voltagem de ativação, Va. Esta voltagem mínima para cada cor de LED correlaciona-se com a energia dos fotões emitidos, Ep (equação 2). E, de facto, como Ep, Va está matematicamente relacionado com a constante de Planck e o comprimento de onda da luz emitida, como se mostra na equação seguinte:
Va = Ep/e + φ/c (2)
onde e é a carga do eletrão (1.6022 x 10−19 coulombs). Para voltagens mais altas do que Va, a corrente elétrica é determinada pela resistência interna do LED. Da Lei de Ohm, voltagem = corrente x resistência, o que produz uma relação linear entre a corrente elétrica e a voltagem aplicada, como se vê nos gráficos voltagem-corrente acima.

cúpulas nas margens do rio
Swan, Perth, Western
Australia.
A imagem é cortesia de
Gnangarra/Wikimedia
Na equação 2, o termo (φ/e) é uma constante que se relaciona com as perdas energéticas dentro da junção p-n do semicondutor. (Por simplicidade, podemos assumir esta contante igual para todos os LEDs.) Uma vez que φ é desconhecido, não é possível, a partir da equação 2, determinar a constante de Planck pela exclusiva medição da voltagem de ativação. Contudo, se a voltagem de ativação for medida para vários LEDs emitindo a vários comprimentos de onda conhecidos, podemos, então, encontrar o valor de h construindo o gráfico de Va como função do inverso do comprimento de onda (1/λ).
Isto acontece porque rearranjando (2) obtemos a equação:
Va = hc/e(1/λ) + φ/c (3)
Assim, o gráfico de Va contra 1/λ tem a forma de uma reta com declive hc/e de onde a constante de Planck pode ser facilmente calculada, dados os conhecidos valores de e e c. O declive pode ser encontrado graficamente representando o dito gráfico e traçando a reta que melhor ajusta os dados, ou, matematicamente, utilizando um calculador de regressão linearw2.
A regressão linear dá o seguinte valor para o declive (m): m = 1.24811 x 10-6Vm (volt metro). Daqui, a constante de Planck pode ser, finalmente, calculada. De cima, m = hc/e e, então:
h = em/c (4)
= 1.6022 x 10-19 x 1.24811 x 10-6/2.9979 x 108
= 6.6704 x 10-34 Js (joule segundo)
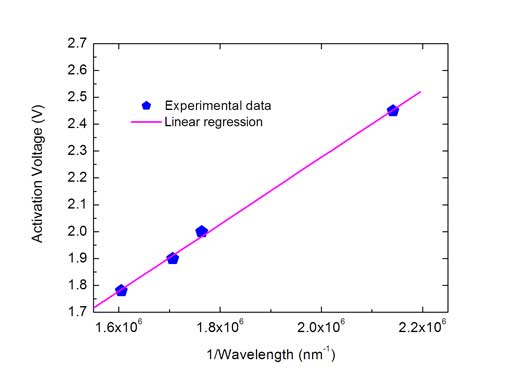
A imagem é cortesia dos autores
Este valor compara-se bem com a constante de Planck, que vale 6.62606957 x 10-34 Js – um erro de apenas 0.7 por centow4. Os valores que os seus alunos obtiverem podem estar um pouco mais longe mas devem, mesmo assim, proporcionar uma satisfatória aproximação a uma das constantes fundamentais da natureza.
Web References
- w1 – Para saber mais sobre a luz e o espetro eletromagnético, ver:
-
Mignone C., Barnes R. (2011) More than meets the eye: the electromagnetic spectrum. Science in School 20:51-59.
-
- w2 – Calculadores de regressão linear online que podem ajudar na análise dos dados incluem:
- w3 – Para aprender como construir o seu espetrómetro, veja:
-
Tiele Westra M. (2007) A fresh look at light: build your own spectrometer. Science in School 4:30-34.
-
- w4 – O valor de referência da constante de Planck pelo National Institute of Standards and Technology (NIST).
Resources
- O projeto ‘Sixty Symbols’ da Universidade de Nottingham produziu um curto vídeo que explica a importância da constante de Planck.
Review
Este artigo apresenta uma experiência simples e prática que pode ser utilizada para verificar o valor da constante de Planck, que é largamente utilizada em Física Quântica. A montagem é facilmente reprodutível em sala de aula, uma vez que os materiais utilizados são comuns em laboratórios de Física. Assim, a montagem pode ser utilizada quer para uma demonstração em sala de aula quer para a realização de trabalhos de investigação pelos próprios alunos.
A teoria envolvida neste tópico pode, inicialmente, parecer abstrata para a compreensão dos alunos, mas a experiência ajudá-los-á a clarificar alguns conceitos e a compreender melhor as teorias envolvidas. Este artigo e a experiência demonstram alguns conceitos muito importantes, tais como:
- o efeito foto-elétrico, onde ‘pacotes de energia’ são absorvidos por um material e, consequentemente, fazem um díodo emitir ondas eletromagnéticas;
- a voltagem de ativação em díodos;
- o cálculo da constante de Planck.
Catherine Cutajar, Malta
