Supporting materials
Download
Download this article as a PDF

How far away are the stars? Explore in your classroom how astronomers measure distances in space.

Look out of a side window of a moving car or train, and you will notice that your view of objects changes with their distance: nearby bushes or trees seem to be rushing by, while a distant tree or building appears to move far more slowly.
This apparent change in position depending on distance is called parallax. You can reproduce the effect by making the thumbs-up sign in front of your face and watching your thumb first with only your left eye, then only your right eye. As you change eyes, your thumb appears to jump sideways in relation to the more distant background imagery – because your two eyes are in slightly different positions. Now stretch your arm as far as it will go and, moving your thumb closer to your face, repeat the experiment of looking with each eye separately at different distances: you will notice that the shift in apparent position increases as the distance between your thumb and your eyes decreases.
This effect has been used for centuries to determine distances in spacew1. In the mid-19th century, astronomers used parallax to work out the first stellar distances. Surveyors also use this kind of measurement to draw accurate maps of the surface of Earth. Currently, the ESA satellite Gaia, which was launched in December 2013, is measuring extremely accurate parallaxes for more than a billion stars in our galaxy, the Milky Way, increasing accuracy by a factor of about 200.
In this article, we describe an activity that explores the way astronomers use parallax to measure interstellar distances by working out the distance of a ‘star’ set up in a classroom. There is also a short web article about the history of parallax measurements, which you can download from additional material sectionw1.
The activity we describe here reproduces the basic geometry of parallax measurements, using simple devices to measure angles. We have successfully used this activity, which takes between 30 and 45 minutes including setting up, with students aged between 13 and 17. In the next issue of Science in School, we will describe a photographic method of using parallax measurements that is even more accurate and astronomically authentic.
For this activity, you will need an instrument for measuring the angles between sight lines – a theodolite (see figure 1), if there is one in your school’s mathematics, physics or geography equipment. If not, we provide instructions here on how to make a similar angle-measuring device from easily available materials.

If you do not have access to theodolites, you can improvise by making the simple devices shown in figure 2. For each one (you will need two), you will need:

The basic set-up can be seen in figure 3. To simplify things, we make all the angular measurements in the plane defined by points A, B and C, which should be parallel to the ground.

Follow the set-up steps below if you are using theodolites:
Alternatively, if you are not using theodolites, follow these steps to make the improvised devices:
Your task now is to determine the distance between your observing point and the star, taking all your measurements only on Earth. Obviously, you can’t just grab your tape measure and stretch it from B to A, since that would mean leaving Earth. We can’t measure the distances to astronomical objects outside our Solar System by flying there.
Instead, we will measure two angles and the length of one side of the triangle ABC, and geometry will help us to find the length of the remaining two sides, AB and AC. With the theodolite at position B, we can measure the angle ABC as follows:
With the improvised devices, the same angular measurements can be performed as follows, first for the device at B:
You now know the angles of view of the star from two different positions on Earth, plus the distance between these positions. So how do we use these results to work out the distance to the star? First, look at the geometry of the situation, shown in figure 4.
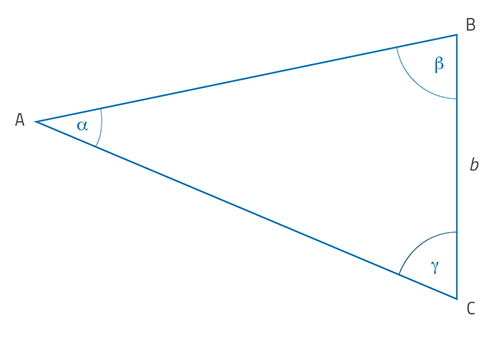
In this arrangement, the star position A and the theodolite positions B and C all lie in a horizontal plane and form the triangle ABC (seen directly from above). Angles b and g are the measured angles ABC and ACB, respectively, and the length b is the measured distance between B and C along the baseline.
Using your own measurements, draw a scale diagram of a triangle like this as accurately as possible: a scale of 1:50 on A3 paper gives good results. Then you can simply measure the distances AB and AC from the diagram, and convert these to real distances to determine the distances of B and C to the star A.
To check your results, break the rules! Travel into ‘space’ and use the tape measure to measure AB and BC.
Finally, discuss the accuracy of the results obtained by angle measurement. If we had used larger distances, how would this accuracy change – and why?

We hope that students will enjoy a sense of discovery from this activity, and get some idea of the way distance measurements are carried out in astronomyw1. Of course, real astronomical procedures use elaborate methods to ensure the best possible accuracy, because the stars are so very far away and their parallax shifts are so tiny. Even our closest stellar neighbour outside the Solar System (Proxima Centauri) is some 100 000 times further away than the longest baseline distance that can be measured from Earth – that is, twice the distance between the Earth and the Sun, if we take images half a year apart. This is like trying to detect a parallax shift in an object 100 kilometres away when we step one metre to the side.
Stellar parallax is the oldest, simplest and most accurate method for determining the distances to stars. This article explains how to make terrestrial measurements using this method. If you follow the instructions, you will be able to measure the distance within your classroom to an object, the ‘star’, and your students will understand how astronomers can calculate huge distances in space.
Corina Lavinia Toma, Tiberiu Popoviciu Computer Science High School, Romania
Download this article as a PDF